硅烯热导率及其拉伸效应的第一性原理研究
通过第一性原理计算和解玻尔兹曼方程研究二维材料硅烯的热导率及其拉伸效应,我们发现硅烯热导率会随着拉伸而成倍增大,这与三维材料热导率随拉伸的变化趋势完全不同。其增大的主要原因是拉伸后声子弛豫时间变大。
随着纳米技术的飞速发展,二维材料显示出优异的光学、电学和热学性质,被认为具有广泛的应用前景。硅烯作为一种典型的二维材料,和石墨烯有相似的结构,而且与后者相比,硅烯和基于硅材料的半导体器件兼容性更好。考虑到无论在实验还是在实际应用中,都很难保证材料内部没有应力存在,研究应力对硅烯热导率的影响很有必要。
一、研究方法
我们使用数值模拟方法来计算硅烯热导率并研究拉伸对其热导率的影响。在一个周期性的晶体结构中,体系的势函数在平衡位置附近的泰勒展开式为:
![]()
其中V0是体系处于平衡位置时的势能,Πi是原子受力,体系处于平衡位置时Πi=0,Φij是二阶力常数,Ψijk是三阶力常数,u是原子的位移。
我们首先通过第一性原理计算优化硅烯结构,然后计算出硅烯的二阶和三阶力常数矩阵。以二阶力常数矩阵作为输入,可以通过晶格动力学方法(对角化动力学矩阵D )计算出声子频率ω,进而可以算出声子热容cph和声子群速v 。以动力学矩阵D的特征值和特征向量以及三阶力常数矩阵为输入,我们分别用弛豫时间近似法(RTA)和迭代法计算出了声子弛豫时间τ。然后通过以下公式计算出热导率:
![]()
其中α和β代表x、y或者z三个方向。N是对第一布里渊区采样的波矢格点的数量。λ代表不同的声子(包括波矢q和声子支ν)。在声子弛豫时间的计算中,我们通过马西森定则计入了三声子散射、同位素散射和边界散射。通过考虑边界散射,可以计算有限尺寸的硅烯的热导率。
对于拉伸的硅烯,我们按特定百分比增大其晶格常数,以此来模拟产生应变。应变大小为ε=(a-a0)/a0,其中a是拉伸后的晶格常数,a0是拉伸前的晶格常数。在计算拉伸的硅烯的热导率时,除了在优化过程中我们保持晶格常数不变之外,其它计算过程与前面完全一致。
在上述所有的计算中,同位素散射过程都被包含了进来。不过对于每一种情况我们都验证了:即使不包含同位素散射,计算出的热导率也不会有很大的变化。
以上的计算方法没有人为选取的参数,计算结果可信度高。
二、研究结果
如图1所示是硅烯结构及其结构参数随拉伸的变化图。从图中我们可以看出硅烯是二维六角蜂窝状结构,有微小褶皱。在拉伸过程中,硅烯的键长不断增大,但是褶皱高度先急剧减小然后趋于不变。在拉伸过程中,褶皱高度与键长的比例在不断减小,硅烯的结构变得更加接近纯平面结构。
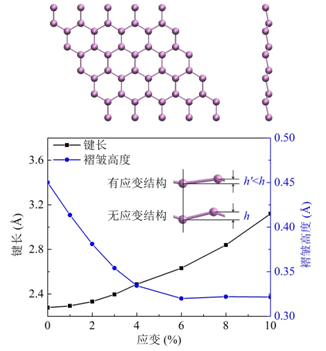
图1 :硅烯结构及结构参数随拉伸的变化
如图2所示是硅烯热导率随拉伸的变化图,其中实线是弛豫时间近似法(RTA)的计算结果,虚线是迭代法的计算结果。我们计算了无限尺寸(图中inf所示)和有限尺寸的硅烯的热导率。
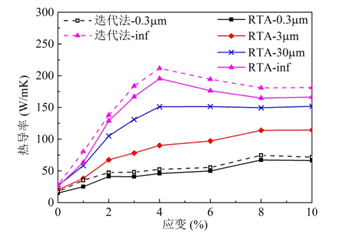
图2 :硅烯热导率随拉伸的变化
对于无限大的硅烯,弛豫时间近似法和迭代法算出的无应变时的热导率分别为25.5 W/mK和27.9 W/mK,两种方法算出的结果很接近。当我们加拉伸应力的时候,两种方法预测的热导率变化趋势相同,都是先成倍增大然后逐渐减小。当拉伸应变在4%的时候硅烯的热导率最高,达到了无应变时的约7.5倍。一般三维材料的热导率会随着拉力增大而减小,而硅烯热导率在拉伸之后增大,而且增大如此之多,这样的结果出人意料。对于石墨烯来说,类似的用第一性原理计算得出的热导率在4%应变时也只增大了一点点。在我们的计算中,最大的热导率出现在4%应变的时候,这与褶皱高度从迅速减小到趋于不变的转折点大致重合,这隐含了热导率与结构上的褶皱高度相关。
对于有限尺寸的硅烯,我们考虑了三种尺寸大小,分别为0.3 μm、3 μm和30 μm。用两种方法计算出的无应变时硅烯的热导率在15-30 W/mK之间,具体值如表1所示,这个结果与XiaokunGu之前的结果吻合得很好。两种方法预测的有限尺寸的硅烯的热导率随拉伸的变化趋势依然相同,所以图2省略了迭代法计算3 μm和30 μm硅烯热导率的结果。有限尺寸的硅烯在拉伸之后热导率也都变大,最大值可以达到无应变时的数倍,拉伸时最大的热导率与无应变时的热导率的比值如表1所示。从表1中我们可以看出在我们考虑的这几个尺寸下,最大增长倍数至少可以达到4.3。对于热导率来说,4.3倍已经是相当大的增长。
表1 :无应变硅烯的热导率和拉伸时热导率的最大增长倍数
| 尺寸 | 弛豫时间近似法 | 迭代法 | ||
| 无应变硅烯热导率 | 最大增长倍数 | 无应变硅烯热导率 | 最大增长倍数 | |
| 0.3 μm | 15.2 W/mK | 4.4 | 17.3 W/mK | 4.3 |
| 3 μm | 20.1 W/mK | 5.7 | 22.4 W/mK | 5.8 |
| 30 μm | 26.9 W/mK | 5.6 | 29.3 W/mK | 5.8 |
因为弛豫时间近似法和迭代法得到的热导率在拉伸下的变化趋势基本相同,而且在弛豫时间近似法中对弛豫时间有更明确的定义,所以后面我们选择使用弛豫时间近似法的结果进行进一步讨论。又因为对热导率起主要作用的是声子的散射,所以后面我们选择无限大的硅烯(只考虑了声子散射的硅烯)的数据进行下一步分析。
从公式(2)可知,弛豫时间近似法计算出的热导率只与声子热容、声子群速和声子弛豫时间三个因素相关。为了找出硅烯热导率在拉伸中变化的主要作用机制,我们以计算无拉伸硅烯热导率的数据为基础,分别将三个参数用拉伸后的硅烯的数据替换掉,来交叉计算出一个热导率的值。比如说,对于在ε应变下将声子热容替换后计算热导率的公式变成:
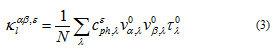
其中ε代表应变大小,0代表无应变的情况。
交叉计算出的热导率如图3所示。从图中我们可以看出在0%-6%这个应变区间,替换声子弛豫时间后的热导率变化最明显,并且远大于其它两个因素的作用,我们可以认为在这个区间起主要作用的是声子弛豫时间。在6%-10%区间,替换声子弛豫时间后的热导率变化约17.8%,而替换声子热容和群速后的热导率变化分别为-12.7%和-5.7%;在这个区间不同因素带来的变化都差不多,三个因素相互制约,最终反映出来就是在这个区间硅烯实际热导率变化不是很大。由前面的讨论我们知道拉伸应变在4%的时候,无限大的硅烯的热导率出现最大值,而0%-6%的应变是声子弛豫时间起主要作用的区间,所以我们可以说硅烯热导率在拉伸时急剧增大的主要原因是声子弛豫时间的增大。
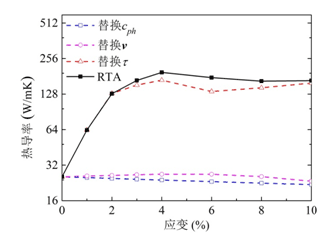
图3 :交叉计算出的热导率
三、结论
综上所述,我们运用第一性原理计算和解玻尔兹曼方程的方法研究了拉伸对硅烯热导率的影响。我们用了弛豫时间近似法和迭代法两种数值计算方法来解玻尔兹曼方程,从而计算出热导率,以上计算方法没有人为选取的参数,因而可信度高。两种计算方法都显示:无论是无限尺寸的还是有限尺寸的硅烯,其热导率在10%的应变范围内都可以增大数倍。这样的趋势与其他材料完全不同,经分析我们发现这其中的作用机理主要是声子弛豫时间的增大。
通讯作者:鲍华,博士,助理教授,上海交通大学。胡明,博士,助理教授,亚琛工业大学。
第一作者:谢涵,博士研究生,上海交通大学。
其他作者:欧阳滔,博士后研究员,亚琛工业大学。ÉricGermaneau,博士,上海交通大学。秦光照,博士研究生,亚琛工业大学。
Email: hua.bao@sjtu.edu.cn鲍华hum@ghi.rwth-aachen.de胡明
参考文献
[1] Han Xie et al., Large tunability of lattice thermal conductivity of monolayer silicene via mechanical strain, Phys. Rev. B, 2016, 93, 075404.
[2] XiaokunGu and Ronggui Yang, First-principles prediction of phononic thermal conductivity of silicene: A comparison with graphene,J. Appl. Phys., 2015, 117, 025102.
[3] Han Xie et al., Thermal conductivity of silicene from first-principles, Appl. Phys. Lett., 2014, 104, 131906.



